前言:由于对面向对象思想认识的不够深刻,所以这一单元的作业写的是非常不oo的,从代码结构来看,结构也显得有些混乱,,没有一个清晰的设计。
作业分析
第一次作业
反思
- 输入 对于三次的作业其实大部分的难点就是在判断输入的合法性上,对于第一次作用来说,最初的想法还是用一整个正则表达式来判断输入,但是这样就会出现爆栈的问题,所以转换思路去匹配每一项,其实对于三次作业我认为正确的判断输入的做法应该是不断的划分到底层在进行正则的合法性的判断,也能够使程序有一定的扩展性,对于第一次来说,可以把项在划分为因子,由于第一次经验的缺少和作业需求的相对简单,所以只在项的层面进行了判断,这就造成了正则形式过于复杂,同时我个人采取的划分表达式的方法是寻找\d[+-]和x[+-],这种方法无疑是只能针对本次作业有效,缺乏扩展性。
- 优化 对于这次的优化,思路也很清楚,就是把相同幂次的系数合并,采用hashmap来存储数据,但是没有在hashmap里使用自定义的类。
出现的bug
由于第一次作业相对简单,所以即便是非常粗糙的代码结构也没有出现很多bug,其中一个bug是因为优化0不输出,所以会出现输出为空的情况,针对这种情况,我才用了输出时进行特判来避免。
代码度量
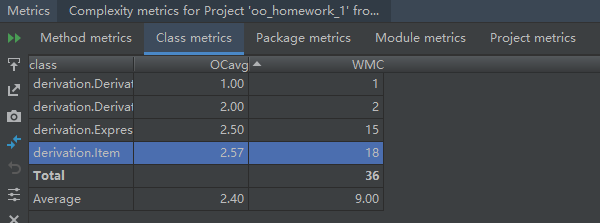
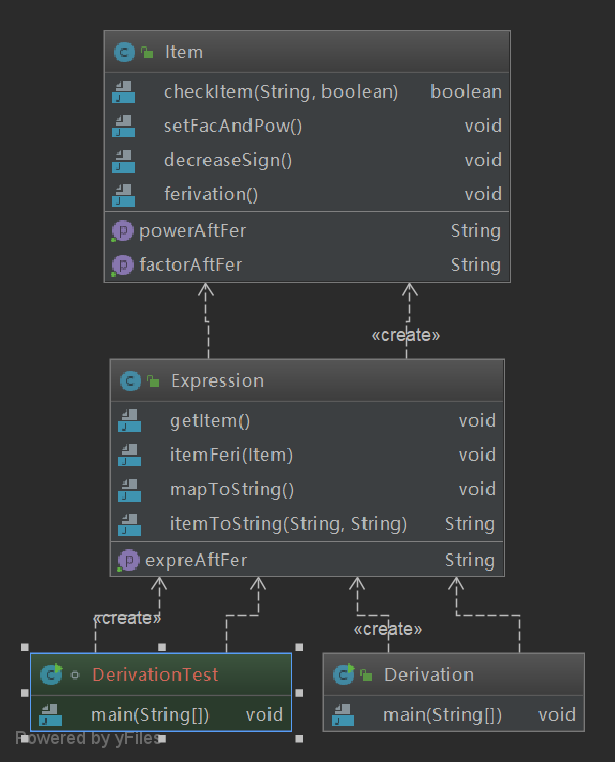
第二次作业
反思
- 输入 第二次的作业,在第一次的基础上增加了sin(x)和cos(x),但本质上还是相乘,所以仍采用了第一次的方法,划分为项然后判断合法性,但是这次项的情况更为复杂,所以项的正则就变得异常复杂,而且难以看懂,同时这种正则也带来了很多bug。
- 求导 由于这次的作业已经不是简简单单的对幂函数求导,所以应用函数求导的法则之后,一个项求导后会变成三个项的和,所以无奈在项的里面加了一个数组来存这三个求导之后的项,并且求导之前的合并系数也变得很麻烦。
- 优化 这次采用了把自定义的类作为hashmap的键,但是由于很菜,并没有对三角函数进行优化。
出现的bug
由于这次没有把item划分为factor,所以导致判断item的正则很复杂,结构对item的判断出现了很多bug,例如sin(x)*,笔者在改bug的时候甚至看不懂原来写的正则。。。
代码度量
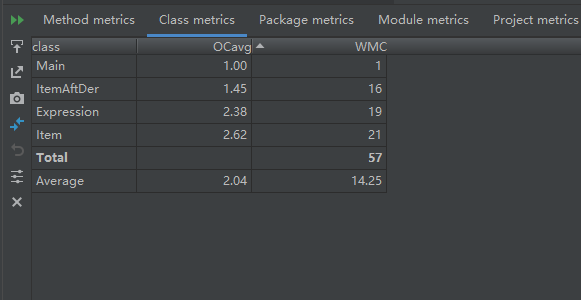
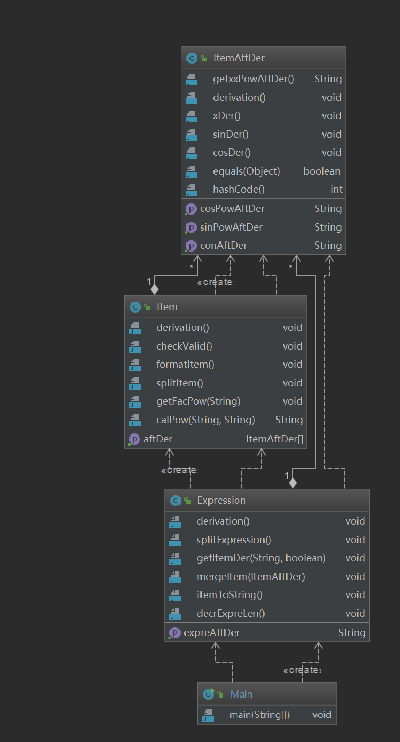
第三次作业
反思
- 输入 这次的作业难度提升幅度巨大,所以之前的方法已经彻底不能再使用,所以经过思考之后,采用树状的形式来储存数据。
- 首先按照加减把表达式分割为项(注意分割时判断加减号是否在一对括号里,以及加减号之前是否有乘号)
- 在按照乘号把项分割为因子(同样需要注意乘号是否在一对括号里)
- 得到的因子如果是被一对括号包围,则是一个表达式因子,继续从1开始判断,否则为基础的常数因子,幂函数,三角函数。
2.求导
因为是采用了树状的结构,所以在求导时也同样在树上求导,使得整个过程变得简化。 3.优化 这次的优化就只做了减少括号,对于0,1的不输出。出现的bug
这次的bug是对可能出现情况考虑的不周全,例如sin(-2)是一个合法的输入,而sin(- 2)就不是一个合法的输入,对于sin内部是否一个因子考虑的不够周全。
代码度量
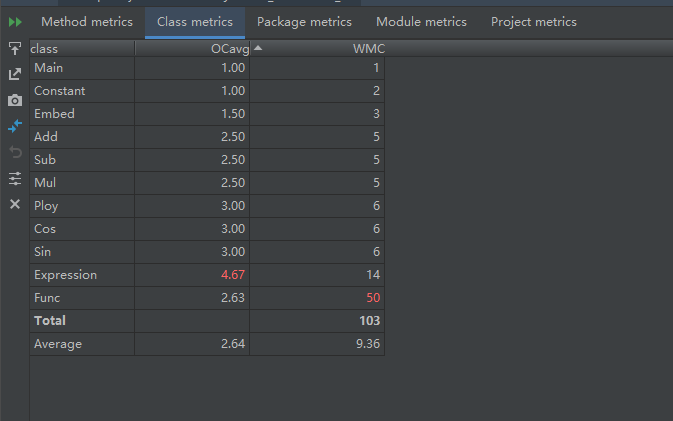
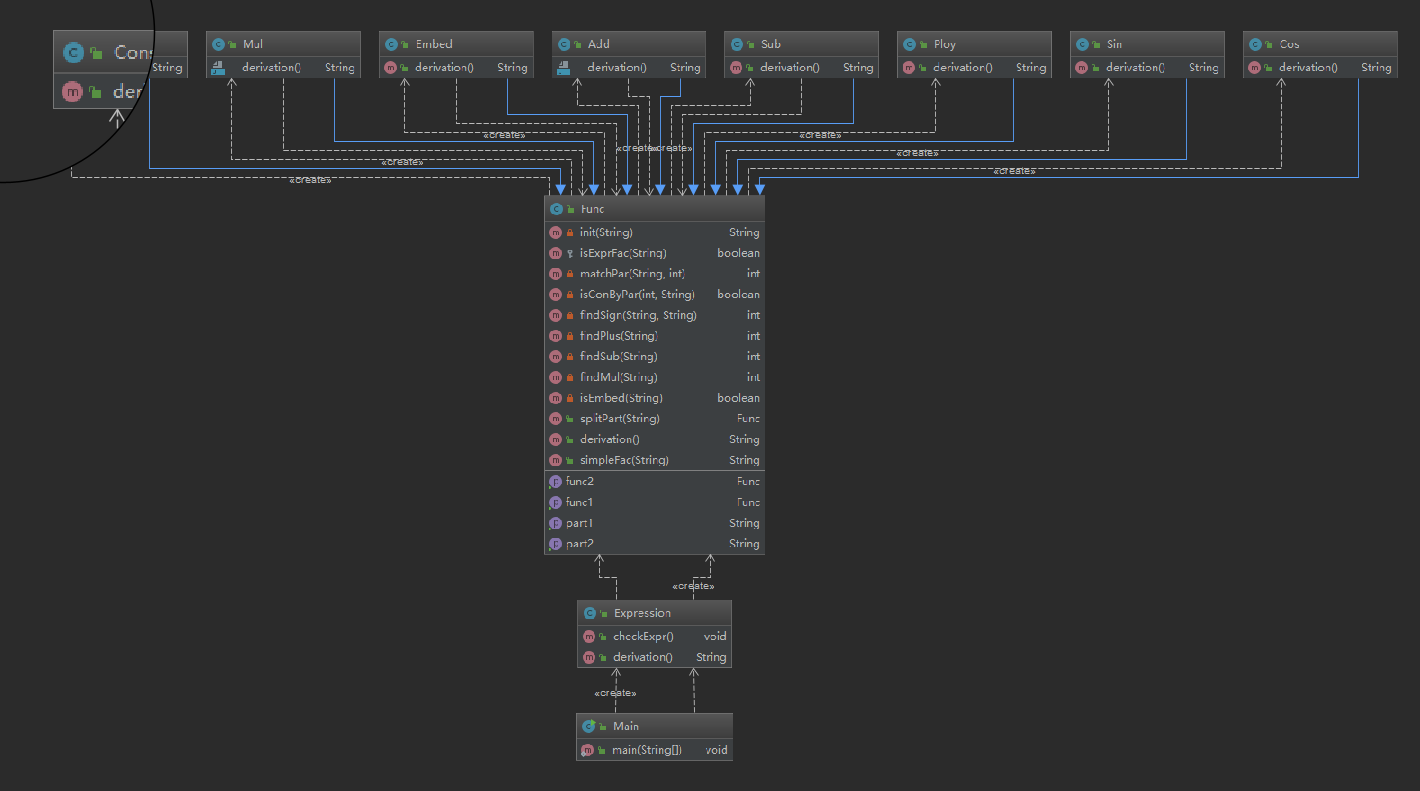
寻找自己程序的bug
主要通过对作业要求的理解,通过脚本生成一些测试,但是当程序的大体逻辑没有问题时,这种方法往往覆盖不到一些特殊点,所以还会手写一些测试数据,但是这些根本上还是依赖于对作业要求理解的完整性。所以与同学交流测试数据也很重要。
发现别人的bug
主要的策略还是读别人的代码,这可能也是互测的根本意义所在,在读别人代码时,也会先用一些自认为特殊的数据先试一试,然后大体过一遍他的逻辑,因为这三次作业,其实大家的处理思路不是一模一样,但有很多的相似之处,所以对与自己处理有很大出入的地方会着重看。
这几周以来的oo的感想
虽然oo非常的紧张刺激,其中可能有很幸运没有被强测找到bug,也会有互测被刀了很多次,也可能有强测直接爆炸,但是最重要的是我们从中学到了东西,如果我们做的不够好,不管这是不是最有效的训练方法,只能说明我们的能力还有很大的不足,就学到东西就好了。